Subnet Calculators: What Are They Good For?

Buckle up and don’t forget to polish your glasses because today we’re getting nittier than gritty. We’re getting: Binary.

Ok, that didn’t make any sense. What we’re really going to talk about is all these Subnet Calculators you’ve seen popping up everywhere. In fact, we just made one ourselves and it’s pretty neat-o.

But what are they really good for?

Well, they tell you just about everything you’ll need to know about an IP address or block of IP addresses.
For instance, do you know what the subnet mask of the IP address “192.168.0.1?” Well, you could calculate it out longhand (which we’ll show you how to do) or you can just plug it into a subnet calculator and have it do all that hard work for you. Afterall, that’s why we invented computers in the first place, right?

Basically, don’t be this guy of the IP world:

Another example (before we get binary) of why an IP calculator is useful is to determine the amount of useable IPs in an IP block, say a /24.

Woah—back up. What the heck is a /24!?

We really didn’t know either, but what that means is there are 256 total IPs in that block, 253 of which are useable. How do we know this? Well, we could have done a ton of math (which we’ll teach you begrudgingly coming up), but really we just plugged it into our calculator and it told us. It also told us the first, last, gateway, broadcast, and network addresses, as well as the wildcard subnet mask!

If you’re reading this, we doubt you wholly understand what any of that means. That’s why you’re here after all—to learn! So, let’s learn!

What Is a Subnet?

A subnet is short for a sub-network and can be defined as a smaller network within a larger one. The smallest subnet is called a broadcast domain whose primary purpose is to route communications between devices on a data network through a device’s MAC address.

What’s a MAC address, you ask? A MAC address, or Media Access Control address, according to Wikipedia is “a unique identifier assigned to network interfaces for communications at the data link layer of a network segment.” They are used for most ethernet and Wi-Fi enabled devices.

However, a MAC address cannot be routed across multiple subnets (or even the Internet) as it’s limited to small networks because it uses ARP broadcasting. ARP broadcasting requires a small network, otherwise large amounts of traffic would bring down the whole network, increasing the broadcast noise (read: it can’t scale).

The most common broadcast domain is a small 8 bit subnet, but there are others which are slightly smaller or larger.
A subnet consists of a Network ID and a Broadcast ID. The Network ID is its beginning number and it’s always an even number. It purpose is to designate the listening address for all devices on the s

ubnet. When someone wants to send data to all devices within a subnet, the use the subnet’s Broadcast ID.
Phew! So that’s a subnet. Pretty understandable. But up there I mentioned the subnet mask, remember? So what’s that?

What Is a Subnet Mask Address?

A subnet mask will “mask” out the host bits, leaving only the network ID visible.
But it does more than that, it also helps to define the size of a particular subnet. Most subnet masks with a bit range of 0 to 8 belong to DSL and T1 IP blocks, while the private network have bit ranges in the 8 to 24 IP blocks.

To figure out all the bit and byte nonsense, head on over to this blog here

However, a subnet mask does more than determine the size of a subnet.

If the IP address on a subnet is known, the subnet mask can be used to determine where the endpoints of that particular subnet are.

But before you can do that, you gotta do some math. Some good ol’ binary conversions. So let’s start:

Binary is all zeros and ones, as I’m sure you’re aware. A subnet mask converted into binary is no different. However, all zeroes are placed on the right while all ones are placed on the left.

LESSON TIME!

CONVERTING IP ADDRESSES FROM DOTTED DECIMAL TO BINARY!

Get out your notepads, people. It’s time for another Colocation America lesson!
Did you know that your computer reads a typical IPv4 address like this: 11000000.10101000.00000001.00000000? That’s binary! Which translates into dotted decimal to something you’re much more familiar with: 192.168.1.0. That’s right—it’s our example IP from the beginning! So how did we get from 192.168.1.0 to that garble of zeros and ones? Let’s take a look at some charts:

128

64

32

16

8

4

2

1

The number in the table above are written as such because each octet of an IP address is made up of 8 bits. We know that in binary, things can only have two values, a “1” or “0.” So, think of the table above as just an exponential representation (called base-8) of the 8 bits in each octet or dotted decimal section.
Take a look at this now:

2⁷

2⁶

2⁵

2⁴

2³

2²

2¹

2⁰

Converting to binary takes a calculation of how many of each number in the table segment above (left to right) fits into the decimal number you have for the IP address (again, going left to right.)

If we take our example IP address, 192.168.1.0 and convert it into binary we have to:

• 128 fits into 192 once with a remainder of 64.
• Since 128 fits into 192 we mark it with a “1” for yes and if it didn’t we’d mark “0”
• In our example, we have a remainder of 64. 64 does indeed fit into 64 with a remainder of zero.
• Following the pattern, our conversion will look like this:

128	64	32	16	8	4	2	1
1	1	0	0	0	0	0	0

Therefore, the dotted decimal segment of 192 is written in binary as 11000000.
The next dotted decimal segment in our example was 168. Using the same formula:

• 128 goes into 168 with a remainder of 40.
• 64 does not go into 40, but 32 does with a remainder of 8.
• Our conversion, then, would be:

128	64	32	16	8	4	2	1
1	0	1	0	1	0	0	0

Therefore, the dotted decimal segment of 168 is written in binary as 10101000.
Now we just complete this for the rest of the dotted decimal segments and we get 11000000.10101000.00000001.00000000.
Pretty simple, but a ton of work. That’s why these calculators are so useful!

CONGRATULATIONS! YOU’VE GRADUATED COLOCATION AMERICA’S DOTTED DECIMAL TO BINARY CONVERSION CLASS! HERE ARE SOME USELESS INTERNET POINTS: “+10”

Now that we know all that, an example of subnet IP address is as follows: a 255.255.255.252 subnet mask has a binary mask that is 11111111.11111111.11111111.11111100. The number of zeros a binary mask has is directly related to the subnet length.

To continue, the subnet for IP address length of the subnet mask 255.255.255.252 is 2. When calculating subnets and subnet masks, there are special numbers that recur and remembering these numbers is essential.

These numbers are 255, 254, 252, 248, 240, 224, 192, and 128.

These numbers are useful for IP networking and help determine where a subnet can be properly broken up into smaller subnets.

See what I mean when I say to use a calculator?

Once the Network ID is found, calculating the Broadcast ID is easy. First, find the subnet length by counting the zeros in the subnet binary form.

Then put 2 to the power of the subnet length to get maximum host for the subnet. With all this information, the range of the subnet can be determined and the Broadcast ID is at the point where the subnet ends.

Now that that’s out of the way, how do you know what your subnet mask is in the first place?

The most simple way is to just plug it into a command line (if you’re using Windows). Just press the Windows Key and “R” simultaneously to open the command prompt and then type “cmd” and press “enter.”

Now, look at the image below and type in the IP config command highlighted by the red box.

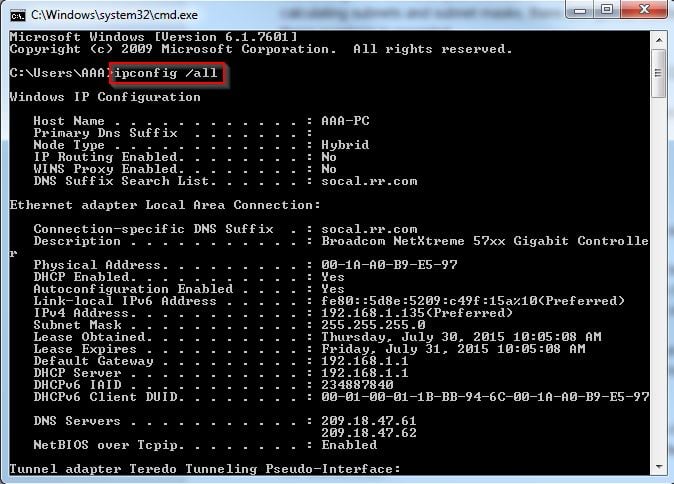
Boom. There’s your subnet mask!

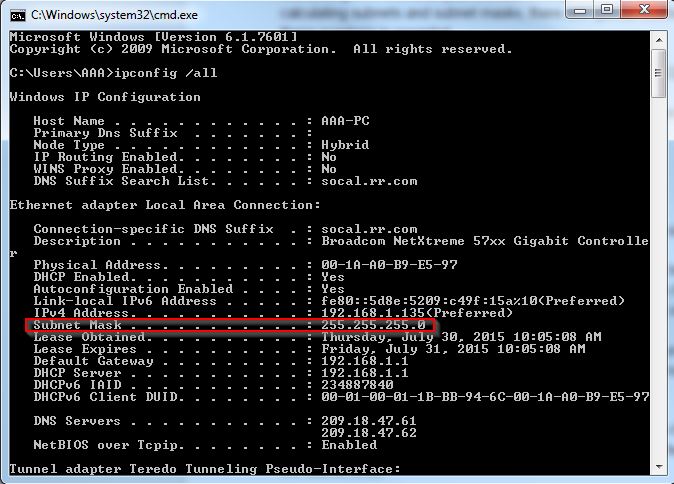
Let’s review by using our example from the beginning of the post.

Understanding an IPv4 Subnet Mask

Now that you understand how much work it would be to convert all this by hand, let’s recall the two subnet masks from the beginning of the post:192.168.1.0 / 255.255.255.0
192.168.1.0/24

The concept of a subnet mask is simple. You have a network and you have hosts on the network (anything with an IP address is a host). The subnet mask determines what portion of the TCP/IP address represents your network and what portion can be used for your hosts. Because I am a simple person, I think of it like this; The network number represents the street I live on, and the host portion is used for the numbers on all the houses on my street.

A subnet mask of 255.255.255.0 means that the first three octets of the address will be used for the network, and thus our network number is 192.168.1. This means we can have 254 computers on this network, because the fourth octet is not being used by the network portion of the address. We know this because of the 0 in the subnet mask (255.255.255.0). We call each of the number sections an octet because we think of them in binary, and there are eight possible bits in each section. Eight bits is an octet. 11111111 in binary is 255 in decimal (did you do the conversions?). So our decimal subnet mask 255.255.255.0 displayed in binary is going to be:
11111111.11111111.11111111.00000000

If you count all the ones, you will find that there are 24 of them. Now look at the subnet mask examples again.

192.168.1.0/255.255.255.0
192.168.1.0/24

Do you see why both subnet masks are the same? The number 24 is the number of bits used in the network portion of the address, and is shorthand for writing the address/subnet mask combination. It becomes important to understand this when you start dividing your network into multiple sub networks.

Long story short, just use a subnet calculator, please. It’ll save you a ton of time.
But we’re all about learning, so we hoped you learned something today. If you have any questions you can reach out to me at [email protected] or leave a comment below!